Welch's method (or the periodogram method) for estimating power spectra
[36]
is carried out by dividing the time signal into successive blocks, and
averaging squared-magnitude DFTs of the signal
blocks. Let ![]() denote the
denote the ![]() th block of the signal
th block of the signal ![]() ,
and let
,
and let ![]() denote the number of blocks. Then the PSD estimate is given by
denote the number of blocks. Then the PSD estimate is given by
However, note that ![]() which is circular autocorrelation.
To avoid this, we use zero
padding in the time domain, i.e., we replace
which is circular autocorrelation.
To avoid this, we use zero
padding in the time domain, i.e., we replace ![]() above by
above by ![]() . However, note that although the ``wrap-around problem'' is fixed,
the estimator is still biased. That is, its expected
value is the true autocorrelation
. However, note that although the ``wrap-around problem'' is fixed,
the estimator is still biased. That is, its expected
value is the true autocorrelation ![]() weighted by
weighted by ![]() . This bias is equivalent to having multiplied the correlation
in the ``lag
domain'' by a triangular window (also called a ``Bartlett window''). The
bias can be removed by simply dividing it out, as in Eq. (E.2).
However, it is common to retain this inherent Bartlett weighting since it merely
corresponds to smoothing the power spectrum
(or cross-spectrum)
with a sinc
. This bias is equivalent to having multiplied the correlation
in the ``lag
domain'' by a triangular window (also called a ``Bartlett window''). The
bias can be removed by simply dividing it out, as in Eq. (E.2).
However, it is common to retain this inherent Bartlett weighting since it merely
corresponds to smoothing the power spectrum
(or cross-spectrum)
with a sinc![]() kernel; it also down-weights the less reliable large-lag estimates, weighting
each lag by the number of lagged
products that were summed.
kernel; it also down-weights the less reliable large-lag estimates, weighting
each lag by the number of lagged
products that were summed.
For real signals, the autocorrelation is real and even, and therefore the power
spectral density is real and even for all real signals. The PSD ![]() can interpreted as a measure of the relative probability that the
signal contains energy at
frequency
can interpreted as a measure of the relative probability that the
signal contains energy at
frequency ![]() .
Essentially, however, it is the long-term average energy density vs. frequency
in the random process
.
Essentially, however, it is the long-term average energy density vs. frequency
in the random process ![]() .
.
At lag zero, the autocorrelation function reduces to the average power (root mean square) which we defined earlier:
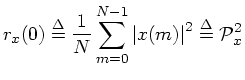
Replacing ``correlation'' with ``covariance'' in the above definitions gives the corresponding zero-mean versions. For example, the cross-covariance is defined as
![$\displaystyle \zbox {c_{xy}(n)
\isdef \frac{1}{N}\sum_{m=0}^{N-1}\overline{[x(m)-\mu_x]} [y(m+n)-\mu_y]}
$](Welch's Method for Power Spectrum Estimation-Dateien/img1499.png)
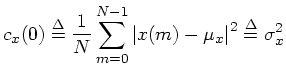
 (automatic links
disclaimer)
(automatic links
disclaimer)