FFT Properties
3.5
The basic tutorial
on frequency analysis
The tutorial is based on the experimental point of view. It is meant to be used together with the software: FFT Properties 3.5. This tutorial does not include any formalized definitions and formulas, because those are available in any DSP book. Tutorial focuses on application of the FFT based frequency analysis and related issues. Any special pre-knowledge is not required, but only the synthesis of theory and application will give the reader a chance to make the best of it.
2.
Periodicity
8. Sum and difference frequencies.
FFT and signal type.
When the program starts, you should switch to the FFT Panel, check off the Sound check button and set Sample time to 1000 ms, then Switch to Signal Generator panel and set the amplitude and the frequency of the signal 1 to 1. You should now be looking at this:

At first it may seem as though there is not much to tell about the upper chart. It is a frequency spectrum of the signal with frequency of 1Hz and amplitude of 1V. The picture of time signal that has produced that frequency spectrum is also very straightforward:

However, a closer observation shows
that frequency spectrum shows frequencies that are not actually present in the
original signal (the triangle):

It seems as if there have been some frequencies present in the original signal between 0 and 1 Hz and 1 and 2Hz. This is of course not true. The reason for such an impression is simply the resolution at which the spectrum is sampled. The spectrum resolution is displayed over the spectrum and yields: 1Hz/lin. That means, that there is one point of data for each Hz from left to the right. Therefore we have points calculated at: 0, 1, 2 .... , 127. This is the cause for the triangle and apparent additional frequencies. The mystery is what amplitudes are between the currently calculated lines. There is a way to sample the spectrum at a desired number of lines. That parameter is defined on the FFT Control page and is called zero padder. Increase the frequency to 20 Hz and set zero padder to 16 and observe the result. (zoom in around 20 Hz, by dragging a rectangle from top-left to bottom-rigth).

We now see what was between the lines. In the original setting (zero padder = 1) we saw a spectrum sampled only at each integer frequency. We can see from the upper picture, that only at each integer frequency the amplitude is zero. We were mislead with the original spectrum. The problem is obvious. We have a whole lot of frequencies displaying that are not there present in the signal at all. A large part of FFT analysis deals with methods on how to reduce these artifacts called leakage. The reason for leakage was already explained in the “The theory and praxis of DFT” (Another document included with FFT Prop). This is also called Gibbs phenomena. The thing to keep in mind: it is always good to have zero padding set to at least 2. This ensures that we will not miss anything.
Now let's change back to zero padding 1. What would happen if the actual frequency would not coincide with the lines at which we have calculated the amplitude? Would we still be able to see the amplitude of that signal? Let us change the original signal frequency to 20.5 Hz. (Change frequency of the signal 1 to 41Hz and set frequency divide to 2 and take a look at the picture:

It seems that there is a whole bundle of new frequencies. Besides, the amplitude does not show the actual amplitude of the signal. It has been greatly reduced. Be warned. This is called leakage, but has nothing to do with leaking of energy. The energy is still there where it was. This is all the consequence of the sampling of the spectrum: how closely together do we calculate lines. Again, increase zero padding to 16.

We get almost the same picture as with 20Hz. Except that the peak is now at 20.5. There are two good things. The amplitude is now accurate and so is the frequency. Why did we get so distorted picture before? We were sampling the upper function at much less points and got a misleading picture.
Let's change back zero padding 1 and take a look at the same picture with logarithmic scale:

The whole spectrum is polluted by a full bandwidth of frequencies that are not present in the original signal at all. Now that is really something to worry about. What about if we had another frequency present in the signal, let's say at 30 Hz but with amplitude a 100 times smaller. Set Signal 1 amplitude to 100 and of signal 2 to 1. The frequency of the signal 2 being 30 Hz. Here is the spectrum:

As we expected, the original frequency is
polluting the whole spectrum and the 100 times weaker frequency is barely
noticeable. If we had more of them, we wouldn't be able to really tell anything.
But you can also look at it the other way. If that distortion would not be present, then it would be necessary to calculate the amplitude at the known frequency. (For example 4.5) In real world that may as well be: 4.56783231.. . It would be almost impossible to hit exactly. So in this way, we at least get the information that there is something. What actually is there, is for us to find out. Usually we are interested in:
· What is the accurate amplitude of the given frequency.
· What is the actual frequency of peak present in the spectrum.
Both of these things are compromised, as we have seen. If the frequency of the signal falls between two lines, and we do not apply zero padding (spectrum oversampling) it is almost impossible to say what is the actual frequency of that signal or the actual amplitude. And besides, how do we know, that the frequencies are actually those that we can see. As far as we know, that could just as well be one misaligned (non-integer period) frequency instead of more aligned ones.
Switch again back to non-zero padded signal by setting the zero padding to 1. To see how the amplitude changes with the frequency, switch to linear scale (lin button just above a log button next to the spectrum) and change the frequency of the signal 1. Make sure that Peak hold scaling (the little S button next to the spectrum) is active and that Divide Freq. is at least 2. Despite the fact, that the amplitude of the original signal is constantly 1, that peak in the spectrum will occasionally fall even for 36% below 1. The graph below shows a spectrum of signal with frequency of 16.5 Hz and Amplitude of 1V. The maximum of the spectrum was found at the 16 Hz. This is due to the fact that lines are calculated only at: 0, 1, 2, ...., 15, 16, 17..... [Hz] (when zero padding is 1)

Different methods have been developed in the past to make such analysis easier, more accurate and faster. The most well known are Windows. Every single frequency analyzer offers at least three Window functions. But more on Windows later on.
The periodicity
Although we have explore the effect of leakage, it is still not quite clear where does leakage come from. FFT assumes that the signal is periodic in time. What does that mean? If the number of periods is an integer number in the given time signal, then the next peace of the infinite (periodic) series would start exactly at the point where it left of. However, if the number of periods per time signal would not be an integer number, we would see breaks like this:

We can see a discontinuity at approximately 220 ms. If we would circulary shift the time signal to the left (signal can be rotated with a rotate button on the time signal control panel), so that the anomaly would be reach 0 ms, we would see this:

Notice, how the amplitude at zero [ms] is 0 V and at 1000 [ms] the amplitude is approx. 0.9V. The first picture was achieved by simply rotating the signal displayed on the second chart. The points from the end of the time series were inserted at the beginning. And the whole reason for the leakage became obvious. The sharp step causes the additional frequencies. The first and the second chart have exactly the same frequency spectrum. This is because we are both times looking at the very same signal, from the FFT point of view. If you set: Signal 1 to 11 Hz (in signal generator) and “Divide freq.” to 3 at 256 samples and change the Rotate up-down button the time signal will be rotated by a given number samples. The interesting thing to observe is the frequency spectrum, that does not change, despite to obvious visual changes in the time signal.
Aliasing or ambiguity
Aliasing is the most dangerous effect in frequency analysis, since it can be the cause of the biggest misinterpretations. Let us take a look at the following frequency spectrum:

We have one signal at the frequency of 120 Hz. But is that really so? Change the frequency of the signal 1 to 136 Hz. The peak should have to disappear from the scale. But it does not. When it reaches 127 Hz. The peak starts to travel back and when we reach the 136 Hz, the peak is again at 120 Hz. It gets much worse. Set the frequency of the signal 1 to 376 Hz. Again the same spectrum. This effect repeats itself in the infinity. The FFT algorithm does not cause this. This is the consequence of the way we sample the original signal.
The main problem that we have to deal with, is how to make sure, that the frequencies in our spectrum are not from somewhere above 300kHz and are only shown as a frequency at 120Hz. The solution is very simple. All the frequencies above the upper limit of the spectrum must be filtered out of the signal. This is called a low-pass filtering.
The interesting thing is also, how is the aliasing reflected in the time domain. Let’s take a look at the following signal.

We have one very high frequency signal (1024 samples, 206Hz). But it seems that there are some low frequencies present. (Close to 1.5 Hz). This is not caused by the way the lines are charted. This is a direct consequence of the sampling. A very high frequency is sampled at points that have these values. You can even zoom in and the signal will retain its form. This example has no actual connection with aliasing, but it is a good example on have FFT can see high frequencies as low ones.
Many times, when analyzing real-world signals, we can see a lot of “noise”, a random like frequencies across the spectrum. Unfortunately, this type of noise could be an indication of improperly set low-pass filters. And what we see as noise, are actually very high frequencies wrapped around upper and lower bound of the amplitude spectrum. When sampling your data, you should make sure that the sampling frequency is higher then two times the highest frequency that is physically present in the process being sampled, or an anti-aliasing filter is mandatory or you will not know what are you looking at. It is pointless looking at data until the sampling was done properly.
Windows
Windows are used to manipulate data (original signal) in such a way, that the desired information can be extracted from the spectrum. In the past, zero padding (frequency spectrum oversampling) was not used much, because it requires more (a lot) memory and fast CPUs. Although memory requirements could have been reduced the CPU speed was still a problem. And some windows were designed to avoid the need of zero padding.
The first thing that one must know about windows is that effect of frequency spill around, demonstrated in the first chapter, is a direct consequence of the Window. The bear fact, that the analyzed signal is finite in length, acts like a rectangular Window. We have not applied any transformation, and we already have a window effect. We have already seen how does Rectangular window behave, now we have a chance to try some other things. Remember. We are looking for a spectrum that will show the actual signal frequencies and amplitudes. We hope that windows will get as close as possible.
Hanning window
The following chart shows a signal of frequency 10 with applied Hanning window.

If the array x[] contains the original signal then the Hanning window is applied in the following way:
for i := 0 to (n-1)
do
c :=
0.5×(1 - cos(i×2×Pi/n));
x[i]
:= c×x[i];
end;

Now lets take look at how is with the leakage and amplitude accuracy.
The chart shows zoomed-in peak. If we compare that picture with the zoom from rectangular window, we see that triangle is 4Hz in width and not just 2Hz as with Rectangular window. Is this good or bad? It is bad, because now one frequency, even at integer number of periods, pollutes even more spectrum. The real problem of leakage is not that that we are unable to see the actual frequency and amplitude but the fact that one strong frequency can hide the weeker ones. Let's oversample the spectrum by a factor of 16 and look at it in the logarithmic scale:
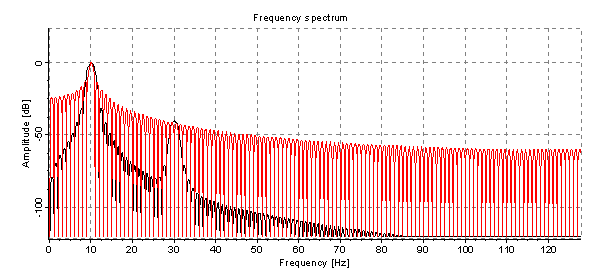
The red series uses rectangular window and the black series was set to Hanning window (FFT Control panel, Window drop down). It is clear to see that the Hanning window affects other frequencies less and that the 30 Hz sine is clearly visible now.
The red line was added to the chart by activating the second channel (check box next to channel 2 on Channels control page). Make sure that Auto scale is active or the display will not be properly aligned. (Popup menu of the spectrum chart - Peak scale - Auto).
Switch to logarithmic frequency would
display this:
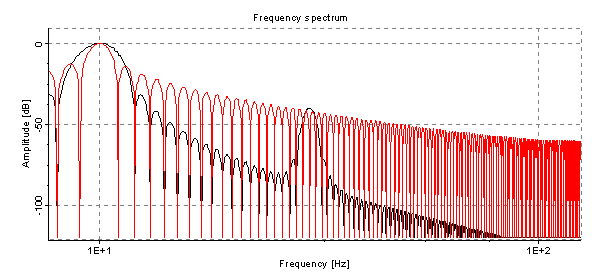
Now we are starting to get an idea of the window behavior. The speed of spectral leakage decay is almost linear with logarithmic frequency and we could talk about dB/decade. And we could talk about the width of the main lobe in percentage of the bandwidth. The rectangular window has a narrower main lobe. Main lobe is the lobe where the frequency is actually present (not leakage).
Let us return to the Hanning window, now, at non-integer number of periods. The frequency of the signal is 10.5 Hz and zero padding is 1 (no oversampling).

I hope that the advantage of the zero padding has now become obvious. If the signal would be zero padded (spectrum sampled at 16 times more lines) the actual frequency could be considerably more accurately read out, not to talk about the amplitude.
But if zero padding is 1 (off): The hanning window is obviously much better, since the biggest error is only 15% instead of 35% as with Rectangular window.

It is obvious that the leakage effect of the hanning window is MUCH smaller then with the rectangular window. The only disadvantage of the hanning window, towards the rectangular, is wider peak when we have integer number of periods. But this is more than sufficiently compensated with higher amplitude accuracy and less leakage. We will see later that wider peak is practically the only way to achieve higher amplitude accuracy if zero padding is off. There has even been a Window developed especially for that purpose. It is called Flat top window.
In practice the Hanning window is the most used one. The reason for it, is its low leakage and simple formula. How does this manifest in practice? Let’s suppose that we have two frequencies present in the signal: one with amplitude 1000 at f = 11.1 Hz and the other with amplitude 1 at f = 50.1 Hz. Spectrum with the hanning window and zero padding off:

Spectrum with the rectangular window:

With rectangular window the second frequency is practically not visible.
Flat top window

This window was especially designed for measurement of the amplitude in the spectrum. But with high spectrum oversampling rates (zero padding) this window has become virtually obsolete.
for
j := 0 to (n-1) do
begin
w :=
2*p*j/n;
c := 0.2810639 -
0.5208972*cos(w) + 0.1980399*cos(2*w);
x[j] :=
c*x[j];
end;
The logarithmic spectrum:

The black line is Hanning and the red line is Flat Top. We see that there is less leakage then with rectangular window and more then with hanning. But then again, this was not the purpose if this window at all. In the worst case the amplitude has only 0.2% numerical error and that without zero padding: The frequency of signal was 35.4 Hz.

All the time from the beginning of frequency analysis the researchers have tried to find a window that would have the smallest leakage. Blackman was one of the first that came really close to that requirement.
It is calculated as:
for j := 0 to (n-1)
do
begin
c := 0.42 -
0.5*cos(2*Pi*j/n) + 0.08*cos(4*Pi*j/n);
x[j] :=
c*x[j];
end;
Blackman window was developed somewhere along with the search for ideal window. That ideal window is today known as Kaiser window. Blackman comes very close to Kaiser window. Kaiser window is rarely used because it requires the calculation of Bessel function of the first kind. This function is not widely known as are those required for calculation of Hanning, Hamming or Blackman windows. Despite the fact, that Kaiser has published the following Fortran code in 1974 to calculate the Bessels function:
REAL FUNCTION
I0(X)
DS=1.0
D=0.0
S=1.0
1
D=D+2.0
DS=DS*X*X/(D*D)
S=S+DS
IF(DS-.2E-8*S) 2, 1,
1
2
I0 = S
RETURN
END

the Kaiser window is not used in today’s frequency analyzers.
And now back to Blackman:
The logarithmic spectrum looks like:

The leakage is little bit smaller than with hanning window, but the peak is even wider:
The amplitude accuracy:

is also a little better then with Hanning window: 11.9% (with zero padding off). (The frequency of the signal is 35.5 Hz). The conclusion would therefore be that Blackman window is the best choice for most of the applications if the Kaiser is not available.
Hamming window
This window was derived from hanning window. The changes were very small but the results are very different. The reason for changes were points just at the beginning and just at the end of the signal. After the hanning Window is applied to the signal, those points are almost zero. That means that we loose the frequencies that were present in that area of the signal. The other, much better solution to that problem, was overlapping. When calculating the spectrums, the time signal always contained also the second half of the data contained in the previous time signal part. The overlapping factor could vary and was usually between 50 and 90%. FFT Properties allow a reach set of overlapping settings on the File input control panel. The hamming window has lost some of it's attractiveness with the procedure. But let’s have a look at the spectrum anyway:

The red line is hamming the the black is the Hanning. We see that the leakage is big (almost as high as with rectangular window) and the amplitude accuracy:

The accuracy (maximum error) is 18.1% (with no zero padding). That is worst than Hanning window and better then rectangular.
Exponential window
When performing dynamic analysis of the system, the so-called system transfer function must be acquired. For that purpose, those values of the time signal towards the end of it must be close to zero or zero. What effect has that procedure on the frequency spectrum can be observed by using that window.
Phase spectrum
FFT originally works with complex data. The output is therefore also complex. The amplitude of the signal is calculated as:
Amplt2 = Im2 + Re2
And the phase analogue:
Phase = arctang (Im/Re)
The phase spectrum of signal at 69 Hz.

Spectrum shows numerical noise. Since at all other frequencies, but the one that is actually there, we have zero, or almost zero, the phase is calculated as something as:
Phase := arctan(0.000000012312./0.00000000321).
To add at least some values to each frequency we can change the frequency to have non-integer number of periods per time signal, or we can add small artificial noise in the form of the delta function. (Check box Phase in FFT Properties). The effect of small artificial noise (rectangular Window):

The effect of non-integer number of periods for the frequency 68.66666 Hz:

The effect of leakage is very evident even in phase. Unfortunately this is not the only picture. The phase changes continuously while the frequency passes between two lines (bins) of the frequency spectrum and is valid only when coinciding with the lines.
It is however interesting to see what happens if we window the function at non-integer number of periods. Change the windows in FFT Properties and see for your self. Unattractive behavior of the phase with non-integer number of periods was the reason for the developers to concentrate on extracting phase from signals with integer number of periods, by specially designed hardware, or transformation of signals, by software (digital resampling) with non-integer number of periods to signals with integer number of periods. FFT Properties offer an alternative to software based order-tracking that traces peaks very accurately. This allows phase extraction within +/- 0.1 degree accuracy with single precision.

If we set DC of signal 1 to 1V, the amplitude of the DC component in the spectrum yields 2 V. This proportion (of 1 : 2) remains the same. And even more. One half of the DC component in the spectrum is exactly: average of the signal. We also see, that changing DC does not have any major effect on the rest of the amplitude spectrum. However, it should be noted, that the DC component in the spectrum resides on the spectrum line 0. The line zero is “reserved« for DC component and does not tell anything about the frequencies contained in the signal.
When analyzing real world signals the DC component is mostly completely useless. On many frequency analyzers the auto scale function, scales the spectrum between the maximum and minimum. Unfortunately the maximum value is usually the DC component and it is about 10 times bigger than any other amplitude in the spectrum. The consequence is, that we don't see anything of interest. In FFT Properties you can check the DC Dump checkbox and the DC component will be removed without any consequence for the rest of the signal. DC Dump is also automatically activated when signals are loaded from files.
The real world signal with DC component present:

The same signal and DC component removed:

Beating
Till now, we have demonstrated all the key features of frequency analysis. But, praxis sometimes brings out things that we did not dare to dream about. In fact, FFT does have problems dealing with frequencies that are very close together, closer than the wide of the peak.
Try the following:
Set Samples to 1024, Signal 1 to f=799 Hz A=1 V, Signal 2 to f=800 Hz, FreqDiv=13, Sample time = 1000 ms, Rectangular window, and click Run on the Time signal panel. Make sure Signal 2 Amplitude = 1 V, Harmonics = Off and Peak Hold button is pressed (the S button). The effect is the strongest, if the window is rectangular. What you should see is one single peak that is rising and falling. This is called beating of Amplitude.

This effect makes it very difficult to measure the amplitude of both frequencies. In practice, the beating of amplitude is a nightmare for anybody who is balancing shafts. But the problem can partially be solved. The resolution of the frequency spectrum is defined simply by: 1/[ms]. This is the difference in Hz between lines and the [ms] is the length of time signal.
Lets take a look at the same picture at time signal length of 90s. (90 000 ms). This is an unrealistic time, but we did put the two frequencies very close together (0.076Hz).

The consequence: two frequencies are now resolved. Their amplitude and frequency can be accurately measured if we apply the Blackman window:

But not everything is quite as it seems. The frequencies of the two signals seem to be wrong. This is the consequence of aliasing. This is a special case where we can actually make use of aliasing. Therefore it is not necessary to sample the whole time signal (practically 10 to 20 s in length), but we can initiate slow sampling (100 Hz) and take in to account that we will get aliasing. Because we know that aliasing is present and we also know, what are the approximate frequencies of real signals, we can measure the frequency and the amplitude of those closely spaced frequencies with higher accuracy.
Sum and difference frequencies.
Set signal generator to Multiply 1&2. Make sure that Signal 1 and Signal 2 have values set (amplitude > 0) .Now the two signals will be multiplicated.
Sum and difference frequencies arise in the process called amplitude modulation. (In radio, they are called upper and lower sidebands.) Passing signals through any non-linear (amplitude dependent) process will cause this modulation because such a process has a multiplicative component. Consider this trigonometric identity: 2cos(a)cos(b) = cos(a + b) + cos(a - b). (Similar identities exist for sines alone, and for combinations.) Sum and Difference frequencies can be generated by multiplying the instantaneous amplitudes of two sinusoids.
When interpreting frequency spectrum on rotary machinery, such non-linearity's in the machine can cause a lot false prognosis, if not interpreted correctly. The operation of multiplication can complicate things quite a lot. There are a number of ways, how two (or more) sources can combine. It is not irrelevant, if this mathematical games can also appear in reality. (Another example: 2cos^2(a) = cos(2a) + 1). A typical amplitude modulated signal:

The frequency spectrum:
